City Connections

You are given a map with cities and one-way-roads. It is possible that two cities are directly linked by more than one road to ensure higher connectivity. Cities are labelled to . Objective is to find the connectivity between city and city . The connectivity of a pair of cities, and , is defined as the number of different paths from city to city . A path may use a road more than once if possible. Two paths are considered different if they do not use the same sequence of roads the same number of times. Your task is to determine the number of different paths between city and city . Since the number may be large, print the result modulo .

Note: Two roads may connect the same cities, but they are still considered distinct for path connections.

For example, there are cities connected by roads as shown in the following graph:

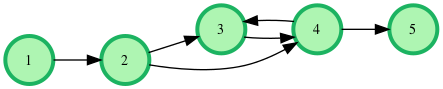
There are two direct paths and one cyclic path. Direct paths are 1->2->4->5 and 1->2->3->4->5. The cycle can be repeated any number of times, so there are infinite paths. If the connection 4->3 did not exist, there would be only the two direct paths.

Function Description

Complete the countPaths function in the editor below. It should print your result, modulo if there are limited paths or INFINITE PATHS if they are unlimited. There is no expected return value.

countPaths has the following parameters:

• n: the integer number of cities
• edges: a 2D integer array where is the source city and is the destination city for the directed road .

Input Format

The first line contains two integers and . Each of the following lines contains two space-separated integers that represent source and destination cities for a directed connection.

Constraints

Output Format

Print the number of different paths from city to city modulo . If there are infinitely many different paths, print INFINITE PATHS.

Sample Input 0

5 5  
1 2  
2 4  
2 3  
3 4  
4 5

Sample Output 0

2

Explanation 0

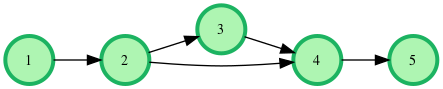
There are two possible paths from city to city :

• 1->2->3->4->5
• 1->2->4->5

Sample Input 1

5 5  
1 2  
4 2  
2 3  
3 4  
4 5

Sample Output 1

INFINITE PATHS

Explanation 1

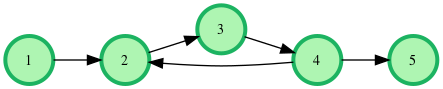
The cycle in the graph can be traversed an infinite number of times on the way to city .

Solution

#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <set>
using namespace std;

const int MOD = 1e9;
int n, m;
vector<vector<int>> graph, reverse_graph;
vector<int> visited, in_stack;
vector<bool> in_cycle, reachable_from_x, reachable_to_y;
vector<int> topo_order;

void dfs_reach(int node, vector<vector<int>> &g, vector<bool> &reachable) {
    reachable[node] = true;
    for (int nei : g[node]) {
        if (!reachable[nei]) {
            dfs_reach(nei, g, reachable);
        }
    }
}

bool dfs_cycle(int node) {
    visited[node] = 1;
    in_stack[node] = 1;
    for (int nei : graph[node]) {
        if (!visited[nei]) {
            if (dfs_cycle(nei)) {
                in_cycle[node] = true;
                return true;
            }
        } else if (in_stack[nei]) {
            in_cycle[node] = true;
            return true;
        }
    }
    in_stack[node] = 0;
    return false;
}

void topological_sort(int node, vector<bool> &visited_topo) {
    visited_topo[node] = true;
    for (int nei : graph[node]) {
        if (!visited_topo[nei])
            topological_sort(nei, visited_topo);
    }
    topo_order.push_back(node);
}

int main() {
    cin >> n >> m;
    graph.resize(n);
    reverse_graph.resize(n);
    visited.resize(n, 0);
    in_stack.resize(n, 0);
    in_cycle.resize(n, false);
    reachable_from_x.resize(n, false);
    reachable_to_y.resize(n, false);

    int x, y;
    cin >> x >> y;
    x--, y--;

    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        graph[u].push_back(v);
        reverse_graph[v].push_back(u);
    }

    dfs_reach(x, graph, reachable_from_x);
    dfs_reach(y, reverse_graph, reachable_to_y);

    for (int i = 0; i < n; ++i) {
        if (!visited[i]) dfs_cycle(i);
    }

    for (int i = 0; i < n; ++i) {
        if (in_cycle[i] && reachable_from_x[i] && reachable_to_y[i]) {
            cout << "inf" << endl;
            return 0;
        }
    }

    // No infinite paths
    vector<bool> visited_topo(n, false);
    topological_sort(x, visited_topo);
    reverse(topo_order.begin(), topo_order.end());

    vector<int> dp(n, 0);
    dp[x] = 1;

    for (int u : topo_order) {
        for (int v : graph[u]) {
            dp[v] = (dp[v] + dp[u]) % MOD;
        }
    }

    cout << dp[y] << endl;
    return 0;
}