Save Rapunzel I

You are playing a game. The game description is as follows:
Flynn Rider needs to save Rapunzel before the witch kidnaps her to another place from this tower. The witch assigned him a mission to free Rapunzel. There are levels in this mission.
Each level must be completed to proceed to the next level. There will be destinations at each level with small tasks to complete. Consider each destination is situated in the number line. Flynn starts at position 0. He can choose any destination, visit it, and finish the tasks. To move to the right cell, you have to press the right arrow button and to move to the left cell; you have to press the left arrow button.
Each button press will move only one cell to the left or right. (He can’t go further left to cell 0) After each level, Flynn will be transferred to the next level, at the same position. (i.e. In the numberline, if Flynn arrived at the final destination, which is at cell , in a level and finished it, then he will be transferred to the next level at cell ).
You are a lazy gamer but a good problem-solver. Can you find the minimum number of button presses to finish all the levels in the mission? You only need to consider button presses to arrive at each destination cell.
Input Format
First line contains the number of testcases. For each test case it will begin with 2 integers & as described in the problem statement. lines will be followed each containing integers. Each integer in the each of these lines represents the cell which contains the task.
Constraints
Length of the number line (Each value of the cell address)
Output Format
For each test case print the minimum number of button presses (i.e. total of left and right button presses) in a new line.
Sample Input 0
1
2 3
3 1 2
2 5 3
Sample Output 0
7
Explanation 0
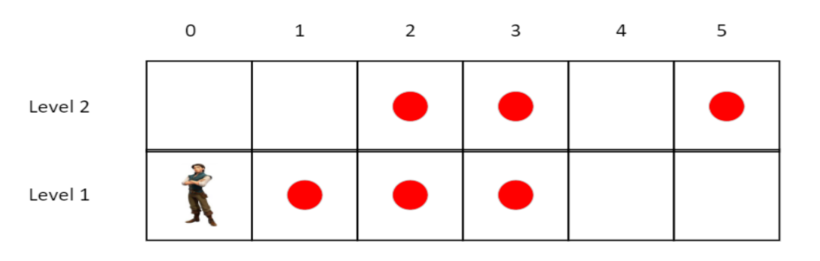
As shown in the figure the red dots are the task destinations for each level. One of the optimal ways to play with a minimal number of moves is,
- Press the right button once & go to destination #1 in the 1st level
- Press the right button once & go to destination #2 in the 1st level
- Press the right button once & go to destination #3 in the 1st level (At this position we have finished the first level & Flynn is transferred to cell 3 in the second level)
- Without pressing any buttons visit destination #3 in the 2nd level
- Press the left button once & go to destination #2 in the 2nd level
- Press the right button three times & go to goal #5 in the 2nd level.
We finished the mission in 7 button presses.
Solution 1
Section titled “Solution 1”By Tharaka Jayasena
#include <iostream>#include <vector>#include <climits>using namespace std;
void dp(vector<vector<int>> &maze, int level, int currentPos, long long currentCost, vector<vector<long long>> &memo);
int main(){ int T; cin >> T; for (int t = 0; t < T; t++) { int N, M; cin >> N >> M; vector<vector<int>> rows; vector<vector<long long>> memo(N, vector<long long>(2, LLONG_MAX));
for (int n = 0; n < N; n++) { int temp, minN, maxN; cin >> temp; minN = maxN = temp; for (int m = 0; m < M - 1; m++) { cin >> temp; if (temp < minN) minN = temp; if (temp > maxN) maxN = temp; } rows.push_back({minN, maxN}); }
dp(rows, 0, 0, 0, memo);
long long minmemo = min(memo[N - 1][0], memo[N - 1][1]);
cout << minmemo << "\n"; } return 0;}
void dp(vector<vector<int>> &maze, int level, int currentPos, long long currentCost, vector<vector<long long>> &memo){ if (level >= (int)maze.size()) return;
vector<int> currentRow = maze[level];
if (currentPos <= currentRow[0]) { long long cost = currentCost + (currentRow[1] - currentPos);
if (currentCost < memo[level][1]) { memo[level][1] = min(memo[level][1], cost);
dp(maze, level + 1, currentRow[1], cost, memo); } } else if (currentPos >= currentRow[1]) { long long cost = currentCost + (currentPos - currentRow[0]);
if (currentCost < memo[level][0]) {
memo[level][0] = std::min(memo[level][0], cost);
dp(maze, level + 1, currentRow[0], cost, memo); } } else {
long long option1 = currentCost + (currentRow[1] - currentRow[0]) + (currentRow[1] - currentPos); if (option1 < memo[level][0]) { memo[level][0] = option1; dp(maze, level + 1, currentRow[0], option1, memo); }
long long option2 = currentCost + (currentRow[1] - currentRow[0]) + (currentPos - currentRow[0]); if (option2 < memo[level][1]) { memo[level][1] = option2; dp(maze, level + 1, currentRow[1], option2, memo); } }}Solution 2
Section titled “Solution 2”By Tharaka Jayasena
#include <iostream>#include <vector>#include <climits>using namespace std;
int main(){ int T; cin >> T; while (T--) { int N, M; cin >> N >> M;
vector<pair<int, int>> rows(N); // {min, max}
for (int n = 0; n < N; n++) { int temp; cin >> temp; int minN = temp, maxN = temp; for (int m = 1; m < M; m++) { cin >> temp; minN = min(minN, temp); maxN = max(maxN, temp); } rows[n] = {minN, maxN}; }
vector<vector<long long>> dp(N, vector<long long>(2, LLONG_MAX)); // dp[i][0] = min cost to reach left end of row i // dp[i][1] = min cost to reach right end of row i
// Base case: from position 0 to first row's ends int left = rows[0].first, right = rows[0].second, width = right - left; dp[0][0] = abs(0 - right) + width; // go to right first, then left dp[0][1] = abs(0 - left) + width; // go to left first, then right
for (int i = 1; i < N; i++) { int prevLeft = rows[i - 1].first; int prevRight = rows[i - 1].second; int prevWidth = prevRight - prevLeft;
left = rows[i].first; right = rows[i].second; width = right - left;
// From previous left to current ends dp[i][0] = min(dp[i][0], dp[i - 1][0] + abs(prevLeft - right) + width); dp[i][1] = min(dp[i][1], dp[i - 1][0] + abs(prevLeft - left) + width);
// From previous right to current ends dp[i][0] = min(dp[i][0], dp[i - 1][1] + abs(prevRight - right) + width); dp[i][1] = min(dp[i][1], dp[i - 1][1] + abs(prevRight - left) + width); }
long long result = min(dp[N - 1][0], dp[N - 1][1]); cout << result << "\n"; } return 0;}