First Order Logic

• Objects: Nouns and noun phrases
• Relations: Verbs and verb phrases along with adjectives and adverbs
• Functions: Relations where there’s only one value for a given input Examples
• Objects: people, houses, Ronald
• Relations: red, round, bigger than, owns
• Functions: father of, best friend, third inning of

Ontological Commitment

The primary difference between propositional and first-order logic is the ontological commitment, that is, what it assumes about the nature of reality. In propositional logic, the statements have only true or false values. In first order logic, assumes that the world consists of objects with certain relations among them that do or do not hold.

Fuzzy Logic: makes the ontological commitment that propositions have a degree of truth between 0 and 1. For example, in fuzzy logic the sentence “Vienna is a large city” might be true to a degree of 0.8 and the sentence “Paris is a large city” might be true to a degree of 0.9.

Temporal Logic: assumes that the facts hold at particular times and that those times are ordered.

Higher-order logic: views the relations and functions referred to by first order logic as objects in themselves

Epistemological Commitments

The possible states of knowledge that it allows with respect to each fact. Fundamental beliefs or assumptions we hold about how knowledge works, what counts as valid knowledge, how we can obtain it and what makes something true or reliable. In both propositional and first-order logic, a sentence represent a fact and the agent either believes the sentence to be true or false or has no opinion. These logic therefore have three possible states of knowledge In systems using probability theory, can have any degree of belief. It’s important not to confuse degree of belief in probability theory with the degree of truth in fuzzy logic.

Models for first order logic

Models link the vocabulary of the logical sentence to elements of possible world. Models of first order logic have objects in them. Domain of a model - set of objects it contains Objects are also called domain elements Relations: tuples of objects that are related Functions should be total functions. (There must be a value for every input tuple)

Symbols and interpretations

Basic syntactic elements of first-order logic

• Symbols that stand for:
  • objects
  • relations
  • functions

Symbols have three kinds:

• Constant symbols (objects)
• Predicate symbols (relations)
• Function symbols (functions)

Total Functions: there must be a value for every input tuple.

Every model must provide the information required to determine if any given sentence is true or false. In addition to its objects, relations and functions, each model includes an interpretation that specifies exactly which objects, relations and functions are referred to by the constant, predicate and function symbols. Ex:

• Richard refers to Richard the Lionheart
• Brother refers to Brotherhood relation

Summary: A model in first order logic consists of a set of objects and an interpretation that maps constant symbols to objects, predicate symbols to relations on those objects and function symbols to functions on those objects.

Terms

A term is a logical expression that refers to an object. Constant symbols are therefore terms. Ex:

• King john’s Left Leg A complex symbol is formed by a function symbol and followed by a parenthesized list of terms as arguments to the function symbol.
• LeftLeg(John)

Atomic sentences

Atomic sentence is formed from a predicate symbol optionally followed by a parenthesized list of terms

• Brother(Richard, John) This states: Richard is the brother of John
• Married(Father(Richard), Mother(John)) Richard’s farther is married to John’s mother

An atomic sentence is true in a given model if the relation referred to by the predicate symbol holds among the objects referred to by the arguments

Complex sentences

We can use logical connectives to construct more complex sentences, with the same syntax and semantics as in propositional calculus. Here are some true sentences:

Quantifiers

Universal Quantification ()

Ex: All kings are persons

Existential Quantification ()

Used for making statement about some objects in the universe

• King John has a crown on his head, (The crown is a crown the crown is on John’s head)

Nested Quantifiers

EX: Brothers are siblings

De Morgans rule for quantified and unquantified sentences

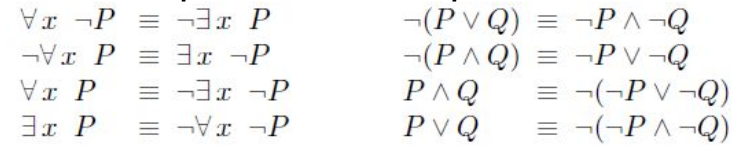
Equality

We can use equality symbol ti signify that two terms refer to the same object

Using first order logic

Domain: some part of the world about we wish to express some knowldege

Assertions and Queries

Sentences are added to a knowledge base using TELL, such sentences are called assertions

• We can ask questions about knowledge base using ASK,
• : returns true If we want to know what value of x makes the sentence true,
• This yields a stream of answers. {x/John} and {x/Richard}. Such answer is called substitution or binding list