Local Search and Optimization

If we want to find the final state instead of the path from start to the goal, we use this method.

Local Search: Searching from start state to neighboring states without keeping track of the paths or the set of states that have been reached.

• Use less memory
• Often can find reasonable solutions in large or infinite state spaces

Optimization Problem: find the best state according to an objective function

Ex:

• Finding a global maximum: hill climbing
• Finding a global minimum: gradient descent

Hill climbing search

Keep track of the current state and on each iteration move to neighboring state with the highest value. Heads in the direction that provides steepest ascent. Stops when it reaches a ‘peak’ where no neighbors have a higher value

Using hill climbing to solve 8-queens problem

• Heuristic function: number of pairs of queens attacking each other (queens can attack same row, column or diagonal)
• Possible states: moving a single queen one move in the same column. (each state has successors) Example state: This state is almost a solution, except for the two queens on column 4 and 7, which can attack each other diagonally. The heuristic for this state would be

The algorithm: Here in this state, the heuristic is 17. We now calculate the heuristic for each queen’s new positions along a column. Now you can see that the lowest possible heuristic we can go-to is 12. There are 8 moves corresponding to this heuristic value. Hill climbing algorithm will pick one of these

Hill climbing is sometimes called greedy local search as it grabs a good neighbor state without thinking ahead.

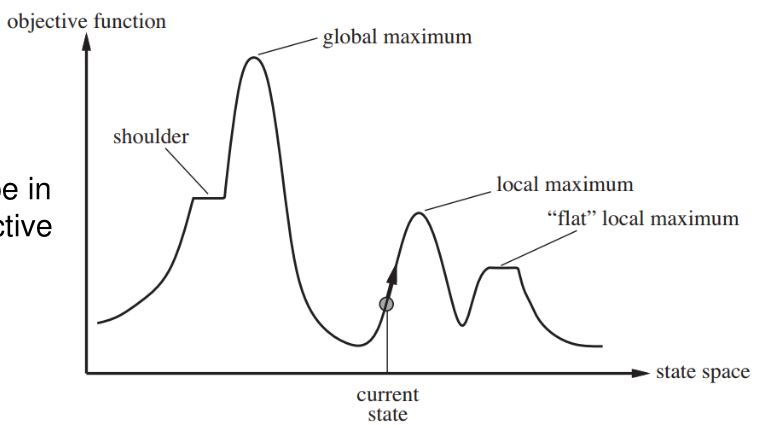
Disadvantages of Hill climbing

• Local Maxima: A peak higher than neighboring states but lower than global maximum
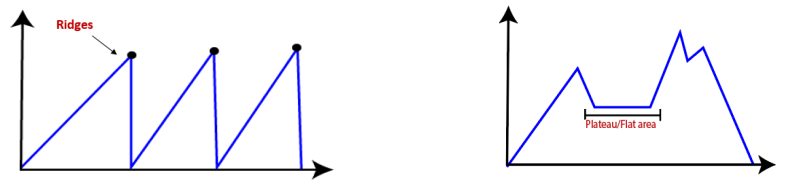
• Ridges: A sequence of local maxima very difficult to navigate
• Plateaus: Flat area of the state-space landscape

Variants of Hill climbing

• Stochastic hill climbing:
  • Choose a random from among the uphill moves. Probability of selection can vary with the steepness of the uphill move.
  • Converge more slowly, but in some landscapes it finds better solutions
• First-choice hill climbing:
  • Implement stochastic hill climbing by generating successors randomly until one is generated that is better than the current state.
  • Good for when a state has many successors
• Random restart hill climbing:
  • Conduct a series of hill climb searches from randomly generated initial states, until a goal is found.
  • Save the best result from any search so far.
  • If all states have equal prob of getting generated, this algorithm is complete with probability 1 (because it will eventually generate a goal state as the initial state)
  • Effective when there are not too many local maxima or plateau.

Simulated Annealing

A hill climbing algorithm that never makes downhill turns is always vulnerable to getting stuck in a local maximum.

Think of getting a ball into a deepest crevice on a bumpy surface. If we let the ball roll, it can end up in a local minimum. We can bounce the ball out of the local minimum and it could go into a deeper local minimum In Simulate annealing we use a temperature (a measure of how hard the shaking is) We start with a higher temperature and gradually reduce the intensity of shaking.

Algorithm:

Similar to hill climbing, instead of picking the best move we pick a random move. If the move improve the situation it’s always accepted. Otherwise the algorithm accepts the move with a probability less than 1.

• Probability decrease exponentially with the “badness” of the move. (amount of elevation worsened).
• Probability decreases as the temperature goes down. Bad moves are allowed more in the start

Local Beam search

Keep track of k states rather than just one. Begin with k randomly generated states. At each step all successors of k states are generated. If any one is goal, the algorithm halts. Otherwise it selects the k best successors from the complete list and repeats.

In local beam search, useful information is passed among the parallel search threads. So this is different from random-restart search.

Stochasitc Beam Search: Choose k successors with the probability proportional to the successor’s value.

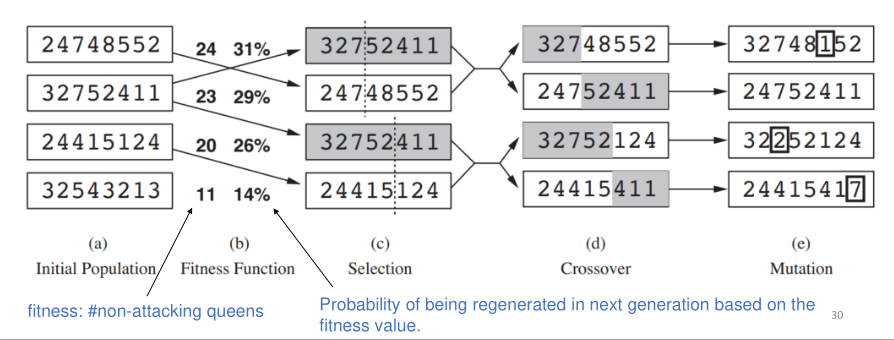
Evolutionary algorithms

Can be seen as variants of stochastic beam search that are motivated by the natural selection in biology. Recombination: In a population of individuals (states), the fittest (highest value) individuals producing offspring (successor states)

• Mixing number (): Number of parents that form offspring
  • if we get stochastic beam search (asexual reproduction)
• Selection: The process of selecting the individuals to become the parents of the next generation
  • Select the most fittest ones as parents
  • or, Select and then select the most fit ones from them
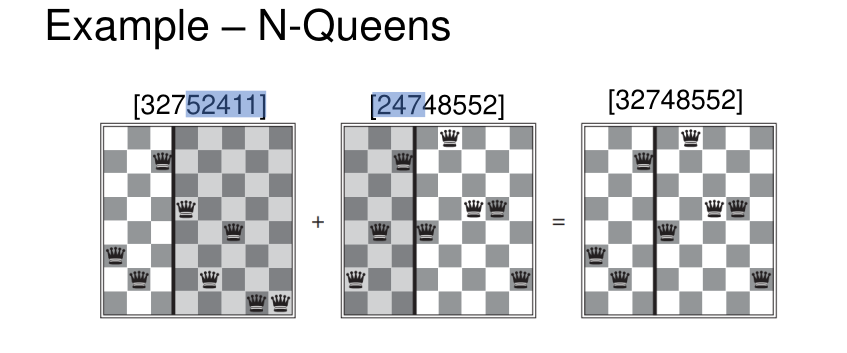
• Crossover Point: The randomly selected point to split each of the parent strings and recombine the parts to form two children
• Mutation Rate: Determine how often offspring have random mutations to their representation. When an offspring is generated, every bit in its composition is flipped with probability equal to mutation rate.
• New generation can consist of new offspring or it can include a few top-scoring parents from previous generation.