Mutual Inductance
1. Introduction to Mutual Inductance
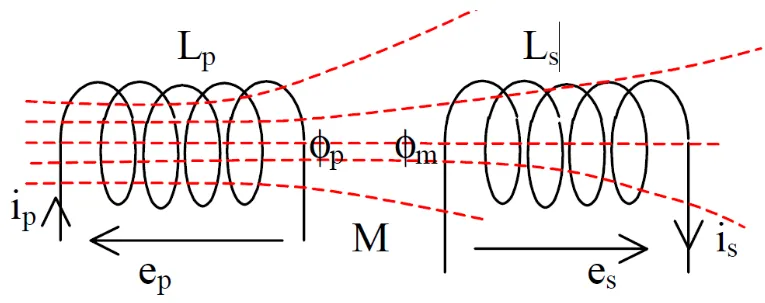
Section titled “1. Introduction to Mutual Inductance”Mutual coupling between coils exists when one coil is in the magnetic field created by another coil.
When a varying current
- A varying flux
is produced in the same coil - This produces a back EMF in the primary coil
- Part of this flux links with a second coil, inducing an EMF
2. Magnetic Field Fundamentals
Section titled “2. Magnetic Field Fundamentals”2.1 Magnetic Flux and Flux Density
Section titled “2.1 Magnetic Flux and Flux Density”The magnetic flux passing through a surface area A:
Where:
= magnetic flux density = differential area element
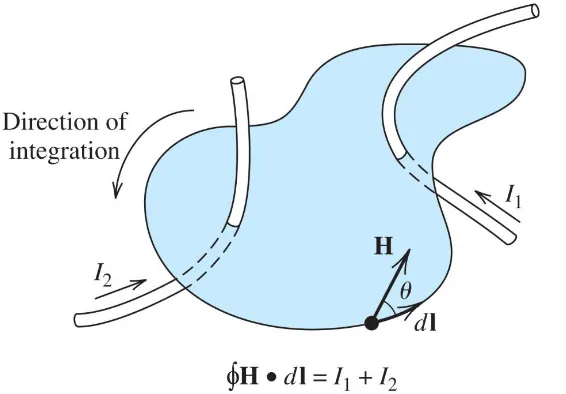
2.2 Magnetic Field Intensity and Ampère’s Law
Section titled “2.2 Magnetic Field Intensity and Ampère’s Law”Relationship between magnetic field intensity and flux density:
Where:
= permeability of the medium = magnetic field intensity
Ampère’s Law:
2.3 Magnetomotive Force and Reluctance
Section titled “2.3 Magnetomotive Force and Reluctance”Magnetomotive Force (MMF) of an N-turn coil:
Reluctance of a magnetic path:
Magnetic Circuit Analogy:
(Similar to Ohm’s law:
3. Mutual Inductance Theory
Section titled “3. Mutual Inductance Theory”3.1 Basic Concept
Section titled “3.1 Basic Concept”When current
- Primary flux:
- Flux linking secondary:
- Coefficient of coupling:
Since
Therefore:
Where
3.2 Mathematical Definition
Section titled “3.2 Mathematical Definition”Important:
3.3 Mutual Inductance in Terms of Dimensions
Section titled “3.3 Mutual Inductance in Terms of Dimensions”For coupled coils with a common magnetic path:
Where
4. Worked Example: Toroidal Coil
Section titled “4. Worked Example: Toroidal Coil”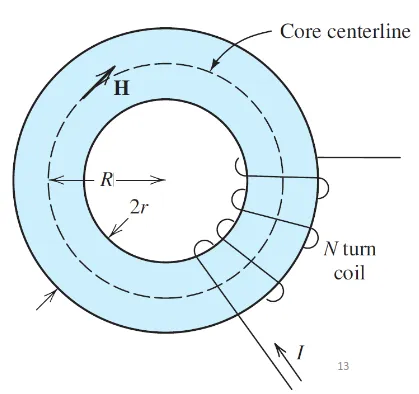
Given: Toroidal coil with N turns, current I, core permeability μ
Find: Magnetic flux density B, total flux φ, flux linkages λ, reluctance ℛ
Solution:
Using Ampère’s law on the center line:
Total flux:
Flux linkages:
Reluctance:
5. Dot Notation Convention
Section titled “5. Dot Notation Convention”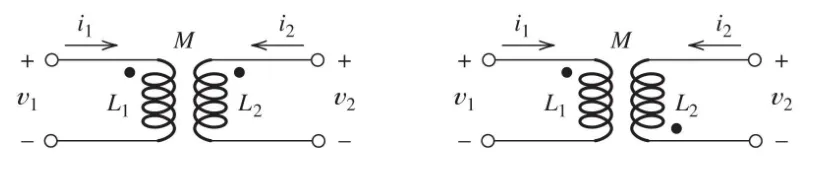
5.1 Rules for Dot Notation
Section titled “5.1 Rules for Dot Notation”Case 1: Both currents enter dotted terminals (or both leave)
- Fields aid each other
- Mutual inductance term has same sign as self-inductance term
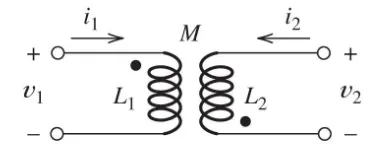
Case 2: One current enters dotted terminal, other leaves
- Fields oppose each other
- Mutual inductance term has opposite sign to self-inductance term
5.2 Voltage Equations with Dot Notation
Section titled “5.2 Voltage Equations with Dot Notation”For two coupled coils:
Aiding fluxes (+M):
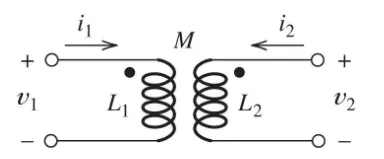
Opposing fluxes (-M):
6. Energy in Mutually Coupled Coils
Section titled “6. Energy in Mutually Coupled Coils”The total energy stored in two mutually coupled coils:
Aiding fluxes:
Opposing fluxes:
General form:
7. Worked Examples
Section titled “7. Worked Examples”Example 1: Mutual Inductance Calculation
Section titled “Example 1: Mutual Inductance Calculation”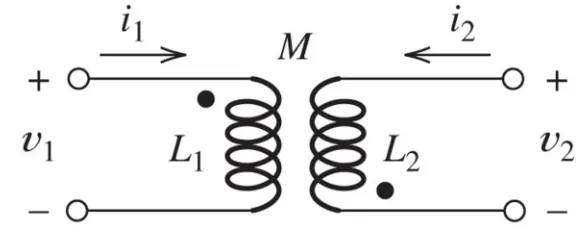
Given:
H, H, H A, A
Find:
Solution:
Example 2: Toroidal Core with Two Coils
Section titled “Example 2: Toroidal Core with Two Coils”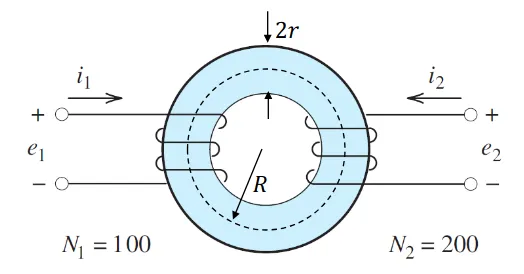
Given:
- Two coils on toroidal core
- Core reluctance:
(AT)/Wb turns, turns
Find: Self-inductances and mutual inductance
Solution:
Self-inductances:
Mutual inductance:
8. Equivalent Circuits for Coupled Coils
Section titled “8. Equivalent Circuits for Coupled Coils”8.1 T-Equivalent Circuit
Section titled “8.1 T-Equivalent Circuit”For coupled coils, we can create an equivalent T-circuit:
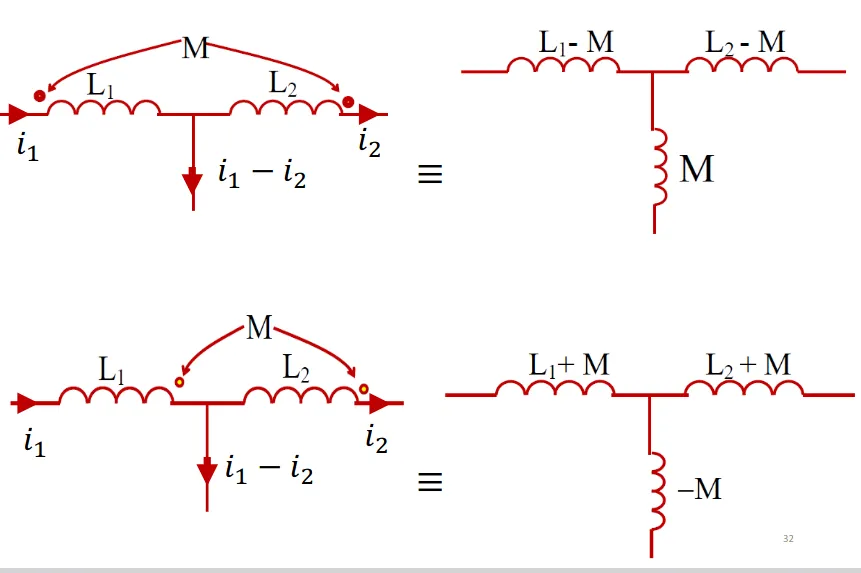
This equivalent circuit eliminates mutual coupling while maintaining the same terminal behavior.
9. Key Relationships Summary
Section titled “9. Key Relationships Summary”| Parameter | Formula | Units |
|---|---|---|
| Mutual Inductance | H | |
| Self Inductance | H | |
| Reluctance | AT/Wb | |
| MMF | AT | |
| Flux | Wb |
10. Important Notes
Section titled “10. Important Notes”- Reciprocity:
- Coupling Coefficient:
- Perfect Coupling:
(all flux links both coils) - Energy Consideration: Total energy must be positive for passive circuits
- Sign Convention: Always use dot notation to determine correct signs