Three Phase Symmetrical Components

What Are Symmetrical Components?

Imagine you have a three-phase electrical system that’s “unbalanced” - meaning the three phases don’t have equal magnitudes or aren’t perfectly spaced 120° apart. This makes analysis very complicated!

Symmetrical components is a clever mathematical trick that breaks down any unbalanced 3-phase system into three simpler, balanced systems that are much easier to work with.

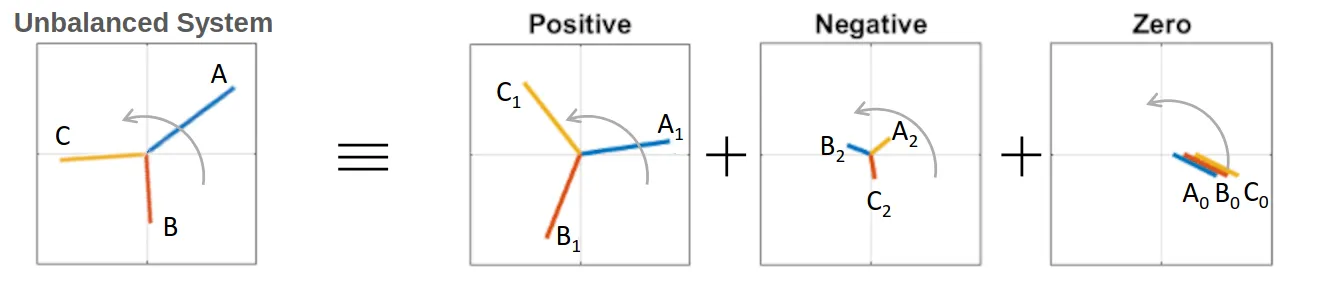
The Three Components

Any unbalanced system can be split into exactly three balanced components:

1. Positive Sequence () - Rotates in the same direction as the original system
2. Negative Sequence () - Rotates in the opposite direction
3. Zero Sequence () - All three phases are identical (same magnitude and phase)

---

Understanding the Magic Operator

Before we dive deeper, we need to understand a special mathematical tool called the operator.

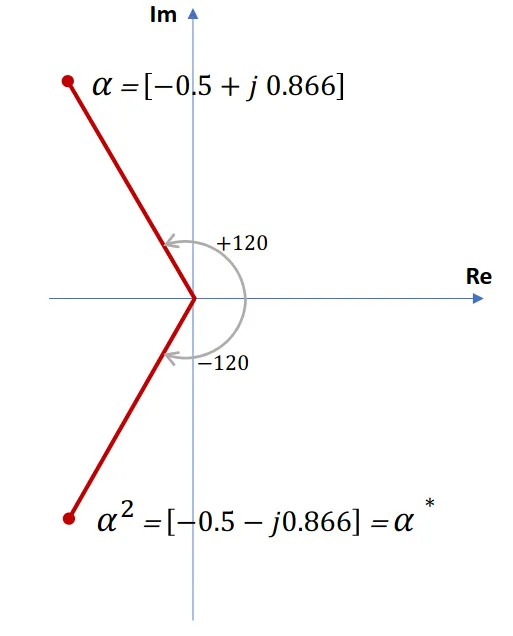
Think of as a “rotation tool”:

• - rotates a phasor by 120° counterclockwise
• - rotates a phasor by 240° counterclockwise
• - back to the original position

In rectangular form:

Key property: (this will be useful later!)

---

The Transformation Equations

Here’s where the magic happens. For any unbalanced system with phases A, B, and C:

Forward Transformation (Unbalanced → Symmetrical Components)

In simple terms:

• - Zero sequence is just the average
• - Positive sequence
• - Negative sequence

Inverse Transformation (Symmetrical Components → Unbalanced)

In simple terms:

---

Worked Example 1: Finding Symmetrical Components

Problem: A 3-phase generator has unbalanced voltages:

• V
• V
• V

Find the symmetrical components.

Solution: Using the forward transformation:

Step-by-step calculation:

1. Zero sequence:
2. Positive sequence:
3. Negative sequence:

Final Answer:

• V
• V
• V

---

Worked Example 2: A More Balanced System

Problem: Another 3-phase generator has:

• V
• V
• V

Solution: Notice that this system is “almost” balanced - the phase angles are exactly 120° apart, but the magnitudes are different.

Using the same transformation:

Answer:

• V (small zero sequence)
• V (large positive sequence - this is the “main” component)
• V (small negative sequence)

Key Insight: Since this system is nearly balanced, most of the energy is in the positive sequence component!

---

Worked Example 3: Reverse Calculation

Problem: You’re given symmetrical components of currents:

• A (no zero sequence)
• A
• A

Find the actual phase currents.

Solution: Using the inverse transformation:

Step-by-step:

Final Answer:

• A
• A
• A

---

Power Calculation with Symmetrical Components

Here’s a beautiful property: the total power can be calculated using just the symmetrical components!

For total complex power:

Or in matrix form:

Why is this useful? You can calculate the total power without converting back to phase quantities!

---

Impedances and Symmetrical Components

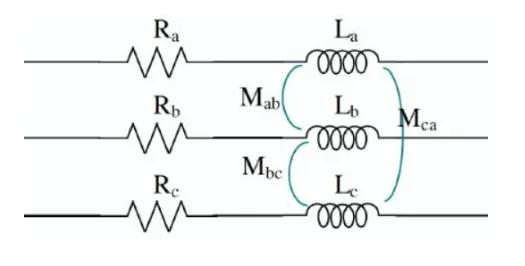
Here’s where things get really interesting for power system analysis:

For Simple Loads (No Mutual Coupling)

Each symmetrical component sees the same impedance. This means:

• Apply each voltage component separately to the load
• Calculate the corresponding current components
• Convert back to phase currents using the inverse transformation

For Complex Systems (Transmission Lines, Machines)

The impedances are different for each sequence:

• Positive sequence impedance () - for normal operation
• Negative sequence impedance () - for reverse rotation effects
• Zero sequence impedance () - for ground current paths

Key Point: This is why symmetrical components are so powerful for analyzing faults in power systems - each type of fault creates different combinations of sequence components!