Transformers

What is an Ideal Transformer?

An ideal transformer is a theoretical transformer with perfect characteristics:

• No copper losses in the windings (zero resistance)
• No leakage flux (all flux links both windings)
• Zero reluctance in the core (infinite permeability)
• No core losses (no eddy current or hysteresis losses)

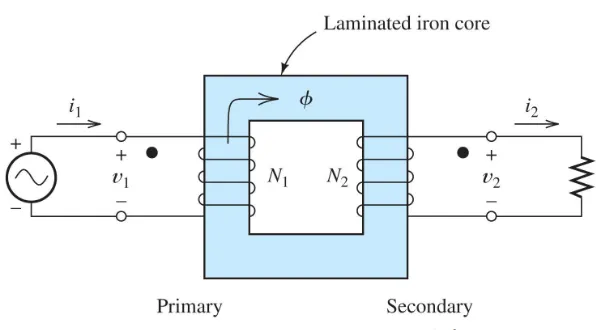
Basic Transformer Equations

Voltage Relationships

For an ideal transformer, the voltage relationship is:

Where:

• = Primary voltage
• = Secondary voltage
• = Number of turns in primary
• = Number of turns in secondary
• = Turns ratio

Instantaneous Voltages

For sinusoidal excitation:

Transformer as Coupled Circuits

MMF (Magnetomotive Force) Balance

The currents and produce opposing magnetic fields. The total MMF applied to the core is:

For an ideal transformer with zero reluctance ():

Therefore:

Current Relationship

The current ratio is inverse to the voltage ratio.

Power in an Ideal Transformer

Power Conservation

In an ideal transformer, no power is lost:

Since (same power factor):

This confirms our voltage and current relationships.

Impedance Transformation

Referred Impedance

An impedance connected to the secondary appears as on the primary side:

Where:

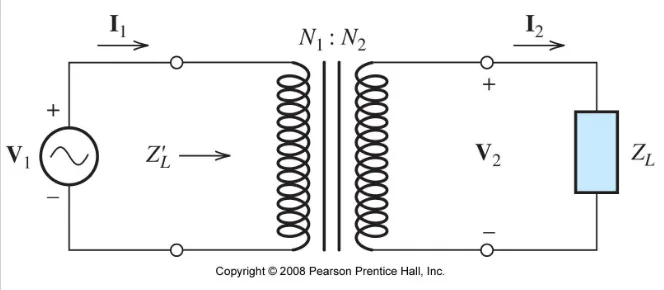
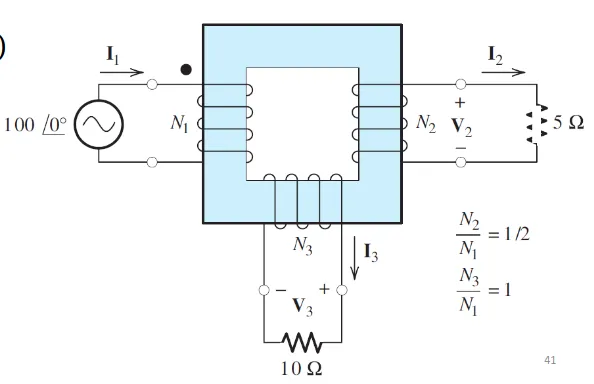
Multi-Winding Transformers

Three-Winding Example

For a transformer with three windings:

Voltage relationships:

MMF balance:

Current relationship:

Polarity and Dot Convention

Dot Notation Rules

1. Voltage polarities: When the dotted terminals are both positive (or both negative), the voltages are in phase
2. Current directions: Currents entering dotted terminals produce MMFs in the same direction
3. Opposing MMFs: For transformer action, currents should enter opposite dot polarities

Practical Example Problem

Given: Transformer with , , Load

Solution:

1. Secondary voltage:
2. Secondary current:
3. Primary current:
4. Power delivered:

Real vs Ideal Transformers

Transition to Real Transformers

Real transformers are modeled as mutually coupled coils with:

Where:

• = Self inductances
• = Mutual inductance
• = Coupling coefficient

Equivalent Circuit Elements

• Leakage inductances: ,
• Magnetizing inductance:

Key Takeaways

1. Perfect transformation: Ideal transformers provide perfect voltage and current transformation
2. Power conservation: No losses in ideal transformers
3. Impedance scaling: Impedances transform by the square of turns ratio
4. MMF balance: Sum of ampere-turns equals zero
5. Polarity matters: Dot convention determines phase relationships