Three Phase Symmetrical Components

Theory of Electricity 2nd Semester

What Are Symmetrical Components?

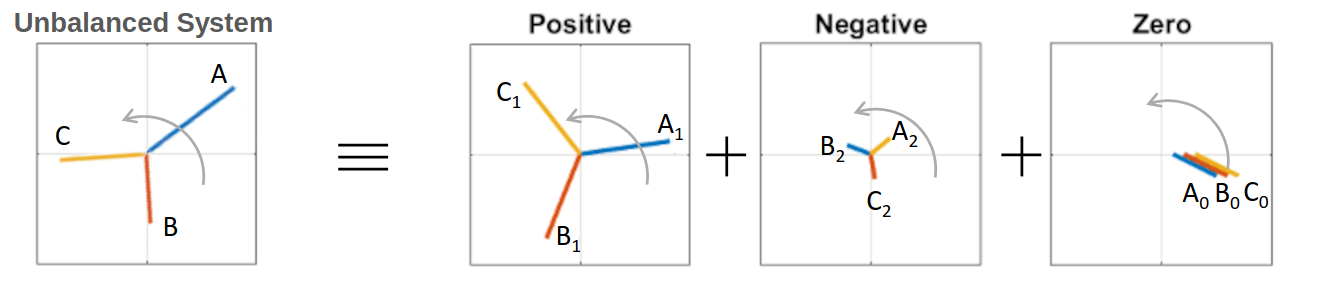
Imagine you have a three-phase electrical system that’s “unbalanced” - meaning the three phases don’t have equal magnitudes or aren’t perfectly spaced 120° apart. This makes analysis very complicated!

Symmetrical components is a clever mathematical trick that breaks down any unbalanced 3-phase system into three simpler, balanced systems that are much easier to work with.

The Three Components

Any unbalanced system can be split into exactly three balanced components:

  1. Positive Sequence () - Rotates in the same direction as the original system
  2. Negative Sequence () - Rotates in the opposite direction
  3. Zero Sequence () - All three phases are identical (same magnitude and phase)

alt text

Understanding the Magic Operator

Before we dive deeper, we need to understand a special mathematical tool called the operator.

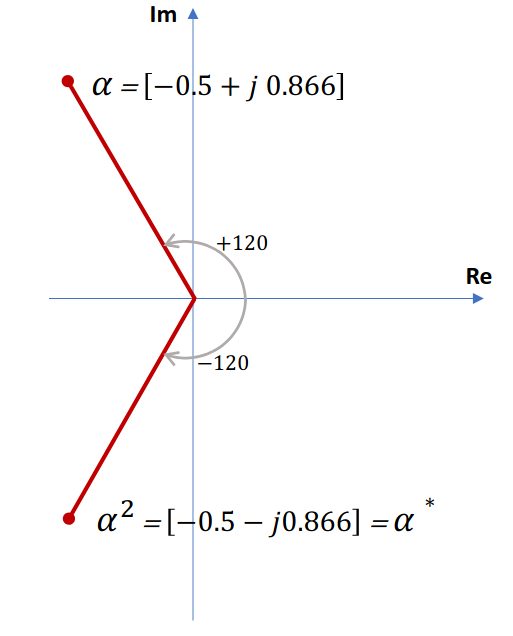
alt text

Think of as a “rotation tool”:

  • - rotates a phasor by 120° counterclockwise
  • - rotates a phasor by 240° counterclockwise
  • - back to the original position

In rectangular form:

Key property: (this will be useful later!)

The Transformation Equations

Here’s where the magic happens. For any unbalanced system with phases A, B, and C:

Forward Transformation (Unbalanced → Symmetrical Components)

In simple terms:

  • - Zero sequence is just the average
  • - Positive sequence
  • - Negative sequence

Inverse Transformation (Symmetrical Components → Unbalanced)

In simple terms:

Worked Example 1: Finding Symmetrical Components

Problem: A 3-phase generator has unbalanced voltages:

  • V
  • V
  • V

Find the symmetrical components.

Solution: Using the forward transformation:

Step-by-step calculation:

  1. Zero sequence:
  2. Positive sequence:
  3. Negative sequence:

Final Answer:

  • V
  • V
  • V

Worked Example 2: A More Balanced System

Problem: Another 3-phase generator has:

  • V
  • V
  • V

Solution: Notice that this system is “almost” balanced - the phase angles are exactly 120° apart, but the magnitudes are different.

Using the same transformation:

Answer:

  • V (small zero sequence)
  • V (large positive sequence - this is the “main” component)
  • V (small negative sequence)

Key Insight: Since this system is nearly balanced, most of the energy is in the positive sequence component!

Worked Example 3: Reverse Calculation

Problem: You’re given symmetrical components of currents:

  • A (no zero sequence)
  • A
  • A

Find the actual phase currents.

Solution: Using the inverse transformation:

Step-by-step:

Final Answer:

  • A
  • A
  • A

Power Calculation with Symmetrical Components

Here’s a beautiful property: the total power can be calculated using just the symmetrical components!

For total complex power:

Or in matrix form:

Why is this useful? You can calculate the total power without converting back to phase quantities!

Impedances and Symmetrical Components

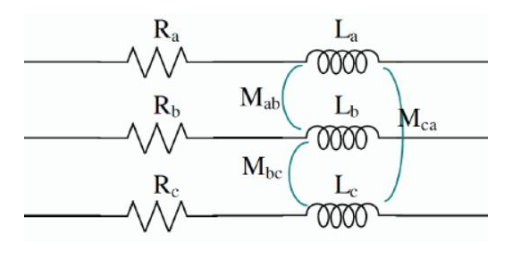
alt text

Here’s where things get really interesting for power system analysis:

For Simple Loads (No Mutual Coupling)

Each symmetrical component sees the same impedance. This means:

  • Apply each voltage component separately to the load
  • Calculate the corresponding current components
  • Convert back to phase currents using the inverse transformation

For Complex Systems (Transmission Lines, Machines)

The impedances are different for each sequence:

  • Positive sequence impedance () - for normal operation
  • Negative sequence impedance () - for reverse rotation effects
  • Zero sequence impedance () - for ground current paths

Key Point: This is why symmetrical components are so powerful for analyzing faults in power systems - each type of fault creates different combinations of sequence components!