Mutual Inductance

1. Introduction to Mutual Inductance

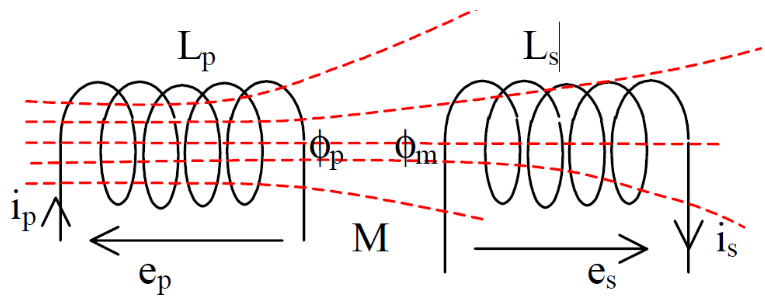
Mutual coupling between coils exists when one coil is in the magnetic field created by another coil.

When a varying current flows in the primary winding:

• A varying flux is produced in the same coil
• This produces a back EMF in the primary coil
• Part of this flux links with a second coil, inducing an EMF

---

2. Magnetic Field Fundamentals

2.1 Magnetic Flux and Flux Density

The magnetic flux passing through a surface area A:

Where:

• = magnetic flux density
• = differential area element

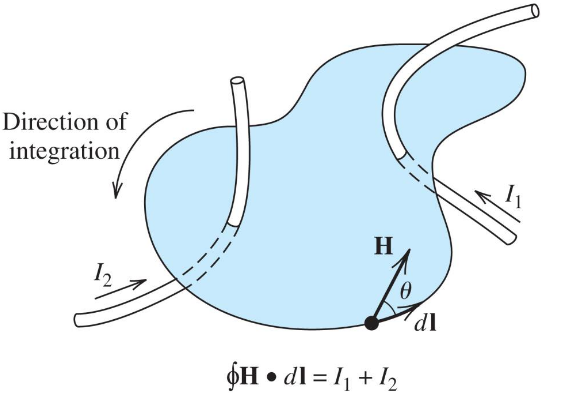
2.2 Magnetic Field Intensity and Ampère’s Law

Relationship between magnetic field intensity and flux density:

Where:

• = permeability of the medium
• = magnetic field intensity

Ampère’s Law:

2.3 Magnetomotive Force and Reluctance

Magnetomotive Force (MMF) of an N-turn coil:

Reluctance of a magnetic path:

Magnetic Circuit Analogy:

(Similar to Ohm’s law: )

---

3. Mutual Inductance Theory

3.1 Basic Concept

When current flows in the primary coil:

• Primary flux:
• Flux linking secondary:
• Coefficient of coupling:

Since and :

Therefore:

Where is the mutual inductance.

3.2 Mathematical Definition

Important: (reciprocity)

3.3 Mutual Inductance in Terms of Dimensions

For coupled coils with a common magnetic path:

Where is the reluctance of the magnetic path.

---

4. Worked Example: Toroidal Coil

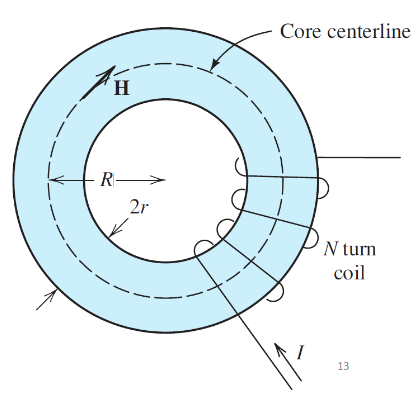
Given: Toroidal coil with N turns, current I, core permeability μ

Find: Magnetic flux density B, total flux φ, flux linkages λ, reluctance ℛ

Solution:

Using Ampère’s law on the center line:

Total flux:

Flux linkages:

Reluctance:

---

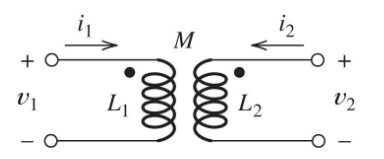
5. Dot Notation Convention

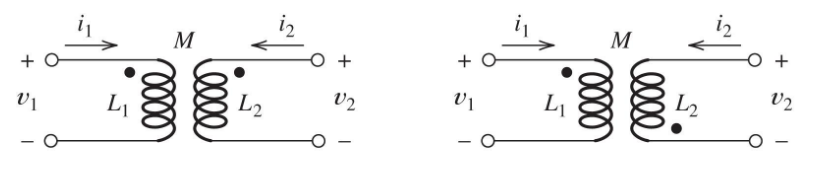
5.1 Rules for Dot Notation

Case 1: Both currents enter dotted terminals (or both leave)

• Fields aid each other
• Mutual inductance term has same sign as self-inductance term

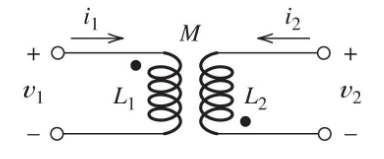
Case 2: One current enters dotted terminal, other leaves

• Fields oppose each other
• Mutual inductance term has opposite sign to self-inductance term

5.2 Voltage Equations with Dot Notation

For two coupled coils:

Aiding fluxes (+M):

Opposing fluxes (-M):

---

6. Energy in Mutually Coupled Coils

The total energy stored in two mutually coupled coils:

Aiding fluxes:

Opposing fluxes:

General form:

---

7. Worked Examples

Example 1: Mutual Inductance Calculation

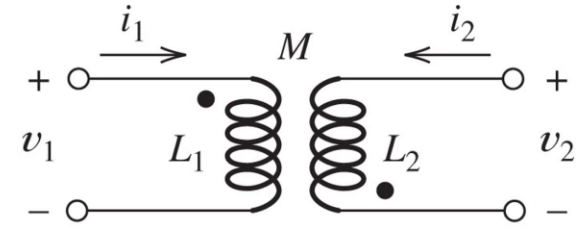
Given:

• H, H, H
• A, A

Find: and

Solution:

Example 2: Toroidal Core with Two Coils

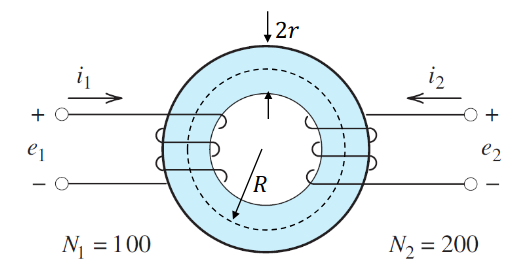
Given:

• Two coils on toroidal core
• Core reluctance: (AT)/Wb
• turns, turns

Find: Self-inductances and mutual inductance

Solution:

Self-inductances:

Mutual inductance:

---

8. Equivalent Circuits for Coupled Coils

8.1 T-Equivalent Circuit

For coupled coils, we can create an equivalent T-circuit:

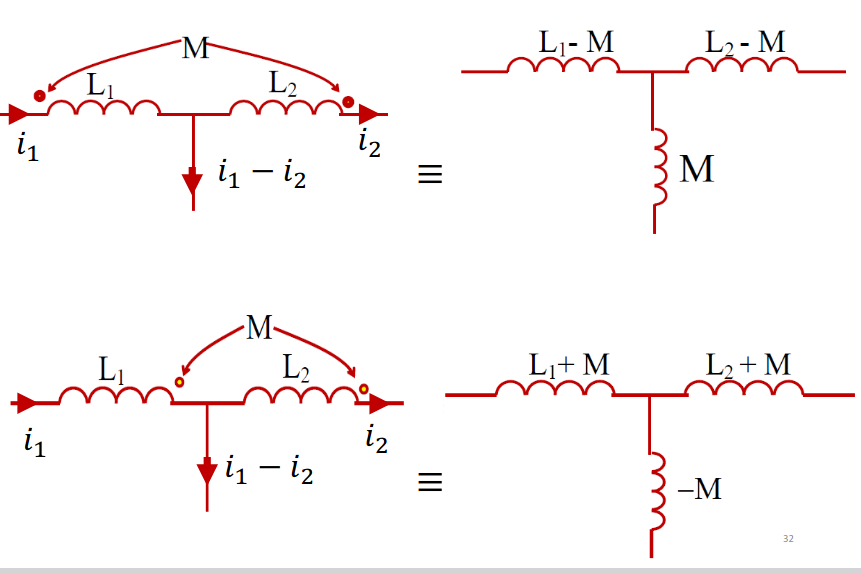
This equivalent circuit eliminates mutual coupling while maintaining the same terminal behavior.

---

9. Key Relationships Summary

Parameter	Formula	Units
Mutual Inductance		H
Self Inductance		H
Reluctance		AT/Wb
MMF		AT
Flux		Wb

---

10. Important Notes

1. Reciprocity:
2. Coupling Coefficient:
3. Perfect Coupling: (all flux links both coils)
4. Energy Consideration: Total energy must be positive for passive circuits
5. Sign Convention: Always use dot notation to determine correct signs